# 前言

我本身并不是学习密码学方向的，所以这里也只是收集整合了一些资料，简单介绍一下密码学方向的学习内容。

纯粹密码学的考题，在 CTF 中会划分到 Crypto 中，有时也会被归于 MISC 的一种，有时会与 PWN、REVERSE 类型的题目相结合。且题目也趋向于前沿化、论文化。

与其它方向相比，Crypto 对自身的数学功底要求很高，很大程度上密码学的难点都是数学问题，尤其是数论的内容一定要掌握。

# 0x00 安全素养

# 网络安全法

不要违法，不要违法，不要违法。

参考资料

https://baike.baidu.com/item/ 中华人民共和国网络安全法

# 0x01 基础

# 需要锻炼的能力

• 数学能力

  学好数学，学好数学，学好数学。

• 识别能力

  能够识别出题目中使用的密码算法或编码算法。

• 攻击能力

  能够结合题目环境设置联想到针对特定算法的攻击方法。

• 分析能力

  能够针对位置算法进行人工分析。

• 编程能力

  能够编程实现破解该算法的程序，并对自己编写的程序的算法复杂度与运行时间有着清醒的认识。

  了解 Python 编程，会写脚本

• 学习能力

  能够快速理解最新文献中的密码学攻击方法并加以实现。

• 跨领域能力

  能够掌握 Reverse、PWN、Web 等其他领域的基础知识。（有时 Crypto 会与其他领域结合）

# 密码学攻击

• 唯密文攻击

  攻击者只拥有密文。

• 已知明文攻击

  攻击者拥有一些与密文对应的明文。

• 选择明文攻击

  攻击者可以进行加密，能够获取指定明文加密后的密文。

• 选择密文攻击

  攻击者可以进行解密，能够获取指定密文解密后的明文。

# 相关书籍推荐

• 《数论盖伦》
• 《深入浅出密码学》
• 《图解密码学》
• 《An Introduction to Mathematical Cryptography》

# CTF 平台

buuoj

攻防世界

bugku

ctfhub

# 学习路线推荐

这里会给出一份学习路线推荐提供参考，实际按照个人情况自由发挥。

作为新手接触密码学，首先从古典密码开始学起，同时还要接触各种新出的、热门的、经典的编码。在 CTF 平台上大量刷题，同时撰写 wp，一些比较生疏的置换密码表要多看几遍，不一定要全记住但需要有个印象。

在古典密码了解比较透彻后，可以开始接触现代密码，首先推荐学习与古典密码关系较大且对数学要求不是很高的的分组密码，把分组密码的五种工作模式以及对应的攻击手段搞清楚。最好是能够自己通过 C/Python 编写程序复现 AES/DES 的加解密过程。

到公钥密码这一块，就对数论基础有较高的要求了，当数论理解了之后，公钥密码也很容易搞懂。这里主要讲以下关于数学的学习，数学是一个长期的过程，不用想着一个月就要搞懂一门，对于计算机学院的同学来说，学院会开设线性代数、离散数学、高等数学等数学课程，如果感觉课上没搞懂，可以看网课继续学习。对数论有了一定基础后，就可以去看一些专门介绍某种加密算法和攻击的论文或者书籍。

如果想在数论方面进一步精进，下面给出一些相关的重点学习内容：

1. 初等数论：整除、同余、二次剩余、原根，并了解有限域上的椭圆曲线。
2. 线性代数：学校教的内容，以及向量空间、子空间、线性变换 / 线性映射的概念。更进阶的话题：对偶空间。
3. 抽代群论部分：重点关注有限群。群、子群、置换群、循环群、陪集与拉格朗日定理（可学群的作用加强理解）、正规子群与商群。同态、同构是代数的重要工具。
4. 抽代环论部分：重点关注含幺元的有限交换环和欧式环。环、子环、理想与商环、多项式环。
5. 抽代域论部分：重点关注 ** 有限域。** 至少能理解有限域上有四则运算。有余力可学域的有限扩张、本原元、~~ 分式域。

# 0x02 密码学

# 编码

编码（encode）的目的不是为了让别人看到后解不出来，而是代表信息的另外一种表达方式。将原始信息转化为编码信息后进行传输，可以解决一些特殊字符、不可见字符的传输问题。接收者接受到编码信息后将其转化为原始信息的过程称为解码（decode）。

编码的用处不仅仅是单独出题，很多时候也为作为题目的一部分，因此掌握编码的识别和转化技巧是学习密码学的基础。

下面是一些 CTF 比赛中常见的编码：

• Hex

  Hex 是最常用的编码方式之一，它会将信息转化为十六进制。

  在进行其他的编码转化时，有时也会先把信息用 Hex 编码再转化。

  Hex 因为比较简单，本身并不会单独出考点，更多时候是用于数据处理。

• Urlencode

  Urlencode 可用于浏览器与网站之间的数据交换，主要是为了解决一些特殊字符的传输过程中产生的问题。

  该编码十分容易理解，即特殊字符在 Hex 编码的基础上，每个字符前置一个 % 即可。

• Morsecode

  摩斯电码应该是最耳熟能详的编码方式，其由长短音构成，在得到一串经过摩斯电码编码的信息后，可以对照密码表得到原始信息。

  摩斯电码通常与 Misc 的音频题结合。

• jsfuck

  jsfuck 的特征十分明显，只要有 ()+[]! 这六个字符组成的的字符串，基本可以确定是 jsfuck 编码。

• uuencode

  uuencode 是把二进制文件转化为可见字符文本的编码。

  经过 uuencode 编码的代码杂乱无章，但是其 ASCII 取值为 32 到 95，因此并不会出现小写字母，所以 uuencode 也比较好辨认。

• base

  base 系列的编码包括 base64、base32、base16 等，其中 base64 最常出现。

  以 base64 为例，其将输入中的每 3 字节（24 比特）按每 6 比特分成一组，编程 4 个小于 64 的索引值，然后通过一个索引表得到 4 个可见字符。

  如果改变了这个索引表中的内容，所得到的编码称为私有 base64，解码方法也是将索引表换成被修改后的私有表，然后解码。也可以用正常索引表解码后当作代替密码解密。

  一般情况下，最后有 = 的编码就是 base 编码，当然 base 编码的最后也可以不含 = 。

  区别 base64、base32、base16 的方式是观察编码中的字符是否位于对应的字符集上。

  base64： a-z，A-Z，0-9，+，/以及补位的=

  base32： A-Z，2-7以及补位的=

  base16： A-F，0-9以及补位的=

# 密码

密码与编码最大的区别就在于密码多了一个关键信息：密钥。

在密码学的学习中，一般用 ** k 代表密钥，用 m 代表明文，用 c ** 代表密文。

# 古典密码

古典密码是最简单的密码加密类型，其对数论的要求并不是很高。在形式上可以分成移位密码和代替密码两类。

古典密码现在已经不再单独作为加密算法使用，但它们是很多现代密码算法的基石。

# 移位密码

移位密码是密码学中最基础的一种密码形式，将明文根据密钥进行位置的变换得到的密文就是移位密码。

• 简单移位密码

  当明文为 m，密钥为 k 时，移位密码会按照 k 的长度来切分 m，然后按照密钥 k 的顺序对每一部分都进行密钥变化，再把加密后的每一部分重新组合，得到密文。

  m="nowyouknowcrypto"

  k="3124"

  先将 m 按照 k 的长度拆分：nowy、oukn、owcr、ypto。

  按照 k 的顺序进行变换，即将原来的第 1 位放到第 3 位，第 2 位放到第 1 位，第 3 位放到第 2 位，第 4 位放到第 4 位，得到：owny、ukon、wcor、ptyo。

  最后组合每一部分，得到密文：ownyukonwcorptyo。

• 曲路密码

  曲路密码先将明文填入一个表中，然后按照一定曲路遍历。

  之前画的图找不到了，用 wiki 的图代替一下。

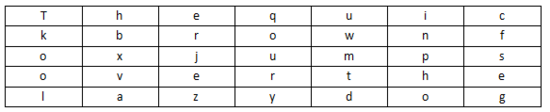
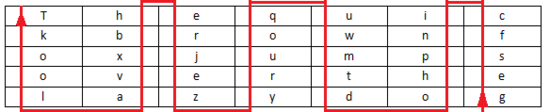
  m="The quick brown fox jumps over the lazy dog"

  c="gesfc inpho dtmwu qoury zejre hbxva lookT"

• 云影密码

  云影密码仅包含 01248 五个数字，其中 0 用于分割，其余数字做加和操作后转换为明文。

  k="abcdefghijklmnopqrstuvwxyz"

  m="120844208481220448041184201428"

  按照 0 划分为 12 、 8442 、 848122 、 448 、 411842 、 1428 。

  解密：1+2=3=c、8+4+4+2=18=r、8+4+8+1+2+2=25=y、4+4+8=16=p、4+1+1+8+4+2=20=t、1+4+2+8=15=o。

  c="crypto"

• 栅栏密码

  栅栏密码是一种规则特殊的移位密码，密钥 k 只有一个数字，表示栅栏的长度。

  在加密时把要加密的明文 m 分为 k 个一组，然后每组的第一个字符依次连接，然后每组的第二个字符依次连接…… 拼接而成的字符串就是密文 c。

  m="nowyouknowcrypto"

  k=4

  把 m 分为 k 个一组：nowy、oukn、owcr、ypto。

  每组第一、二、三、四个字符连接：nooy、ouwp、wkct、ynro。

  拼接在一起得到密文。

  c="nooyouwpwkctynro"

# 替代密码

替代密码首先会建立一个替换表，加密是将需要加密的明文依次通过查表替换为相应的字符，明文字符被逐个替换后会变成无意义的字符串，即密文。替代密码的密钥就是替换表。

如果替换表只有一个，称为单表替代密码；如果替换表有多个，加密过程中依次使用，则称为多表替代密码。

针对替代密码最有效的攻击方式是词频分析。

# 单表替代密码

• 凯撒密码

  凯撒密码通过将字母移动一定的位数来实现加密解密，即明文中所有字母都在字母表上向后（或向前）按照一个固定的数目进行偏移后被替换成密文。

  当偏移值为 3 时，明文中所有字母 A 被替换成 D、B 替换成 E、C 替换成 F，以此类推，然后 W 替换成 Z、X 替换成 A、Y 替换成 B、Z 替换成 C。

  k=4

  m="ABCDEFGHIJKLMNOPQRSTUVWXYZ"

  C="EFGHIJKLMNOPQRSTUVWXYZABCD"

• ROT13

  ROT13 本质上是一种特殊的凯撒密码，当 k=13，且只作用于 A-Z、a-z 时，称之为 ROT13。

• 埃特巴什码

  埃特巴什码与凯撒密码类似，但它的替换表时通过对称获得的。

  ABCDEFGHIJKLMNOPQRSTUVWXYZ 通过镜像对称得到 ZYXWVUTSRQPONMLKJIHGFEDBCA。

  然后用对称后的字母表替换掉原来字符串中的字母，得到密文。

• 培根密码

  培根密码一般用两种不同的字体表示密文，使用 AB 代表两种字体，5 个一组，表示密文。

• 图形替代密码

  即将明文用图形进行代替来实现加密。

  比较经典的有：猪圈密码、跳舞的小人……

# 多表替代密码

多表替代密码的举例过于繁琐，这里只简单讲解一下各个多表替代密码的原理

• 棋盘类密码

  常见的棋盘类密码有：Playfair、Polybius、Nihilist。这类密码的密钥是一个 5x5 的棋盘。

  棋盘的生成有以下条件：

  1. 顺序随机
  2. 不能出现重复字母
  3. i 和 j 视为同一个字（也有去除 q 的，总之要保证总数为 25 个）

  在生成棋盘后，不同的加密方式会用不同的转换方式，这里就不继续深入了。

• 维吉尼亚密码

  维吉尼亚密码是使用一系列凯撒密码组成密码字母表的加密算法，是标准的多表替代密码。

  假设密钥为 CTF，会根据 C、T、F 三个字母在 A-Z 中的偏移得到三个凯撒密码的替换表。然后在进行加密，明文的第一个位置会根据 C 生成的替换表移位加密，第二个位置会根据 T 生成的替换表移位加密，第三个位置会根据 F 生成的替换表移位加密，第四个位置又回到使用 C 生成的替换表移位加密，以此类推。

• 希尔密码

  希尔密码是运用基本矩阵论原理的替换密码。

# 现代密码

# 分组密码

分组密码是将铭文信息编码表示后的 bit 序列，按照固定长度进行分组，在同一密钥控制下用同意算法逐组进行加密，从而将各个明文分组变换成一个长度固定的密文分组密码。简单来说，古典密码中的替代密码是对一个字符进行替换，分组密码则是对一个分组进行替换。

• DES/AES

  DES/AES 属于迭代型分组密码，涉及参数包括分组长度、密钥长度、迭代次数（圈数）、圈密钥长度。

  DES 的分组长度为 64bit，密钥长度为 64bit，圈数为 16，圈密钥长度为 48bit。

  AES 的分组长度为 128bit。当密钥长度为 128bit 时，圈数为 10；当密钥长度为 192bit 时，圈数为 12；当密钥长度为 256bit 时，圈数为 14.

  在 DES 和 AES 中，有两种加解密模式 ECB 和 CBC。其中 CBC 模式的加密会比 ECB 模式多一个初始向量 IV。

# 序列密码

序列密码指将种子密钥通过密钥流生成器产生的伪随机序列与明文简单结合生成密文。其中与明文结合的元素称为密钥流，将产生密钥流元素的部件称为密钥流发生器。序列密码的密码强度主要取决于密钥流发生器的设计。

# 公钥密码

前面所讲的密码的加密密钥和解密密钥都是相同的，从公钥密码开始，加密密钥和解密密钥就不是同一个密钥了。其中加密密钥是公开的，解密密钥是保密的，并且很难由加密密钥推出解密密钥。

说到公钥密码，就不得不提到 RSA，RSA 也是 CTF 比赛中最常出现的公钥密码。

# RSA

学习 RSA，需要具备一定的数论知识，否则很难理解透彻。

这里先过一遍 RSA 加密解密的流程。

小红需要给小刚发送一段隐私信息，但他们之间的通讯通道被小明监听着，因此小红不能直接把信息发给小刚。

于是小刚先挑选两个大素数 p 和 q ，然后相乘得出了 n=p*q ，然后又挑了一个合适的素数 e 。这时小刚把 （n，e） 发送给了小红，当然小明也得知了这个信息。

小红拿到 （n，e） 后，把隐私信息通过 Hex 和 Padding 转换为一串数字 m ，然后通过计算得到 c（c=m^e mod n） ，然后把 c 发送给了小刚，当然小明也得到了 c 。

这时，我们观察一下小红、小刚、小明所掌握的信息：

• 小红：c、m、e、n
• 小刚：c、e、n、p、q
• 小明：c、e、n

当小刚收到小红发送的信息 c 后，通过计算 e 关于 n 的欧拉函数的逆元，求出了 d ，然后通过 d 进行计算就可以算出 m=c^d mod n ，再通过 Hex 的处理就得到了小红发送的隐私信息。而小明没有掌握 p和q ，就无法计算出 d ，从而无法解密 c 来获取 m 。

在上面这个过程中（n，e）就是公钥，（n，d）就是私钥。

下面列出了公、私钥的生成算法和加密解密算法

公、私钥的生成：

1. 随机选择两个不同大素数 p 和 q，计算 N=p*q。
2. 根据欧拉函数，求得 φ(N)=φ(p)φ(q)=(p-1)(q-1)。
3. 选择一个小于 φ(N) 的整数 e，使 e 和 φ(N) 互质。并求得 e 关于 φ(N) 的模反元素，命名为 d，有 ed≡1 (mod φ(N))。

此时，(N,e) 是公钥，(N,d) 是密钥。

信息加密：

1. 先将信息以一个双方约定好的格式转化为一个小于 N，且于 N 互质的整数 m。

2. 对 m 利用如下公式加密

   m^e≡c (mod N)

信息解密：

利用密钥 d 按照如下公式进行解密

​ c^d≡m (mod N)

# RSA 算法的攻击

• 直接模数分解

  正常情况下，攻击者并不知道 p 和 q，因此无法计算出私钥 d 来破解加密信息 m。

  但是如果 n 的取值过小，攻击者可以通过爆破的手段分解得到 p 和 q，从而破解出密文。

• 费马分解和 Pollard_rho 分解

  当 n 的取值过小时，可以通过直接模数分解得到 p 和 q。但即使 n 的取值很大，而 p 和 q 差距过远或者差距过小时，也会产生问题。

  其中费马分解适用于 p 和 q 差距过小的情况，Pollard_rho 分解适用于 p 和 q 差距过大的情况。

• 公约数模数分解

  如果在进行了两次信息传递时，使用的两个大素数 p 和 q 有一个是相等的，攻击者就可以通过对两次通信的 n 进行求公约数的计算进而分解出两次通信的 n，即 n1 和 n2。n1 和 n2 具有一个共同的素因子 p，这是通过 n1、n2 分别去除素因子 p 就可以分解出两次使用的素数 q1 和 q2，然后可以解密了。

• 小指数明文爆破

  如果生成公钥时使用的 e 太小，并且要传输的信息也很小时，就会出现 m^{e＜n 的情况，这时直接对 c 开 e 次根号就可以得到明文 m。如果 m}e＞n 但没有超过 n 太多，即 k*n＜m^{e＜(k+1)*n，当 k 处于可以爆破的大小时，可以通过关系式 k*n-c=m}e 来爆破明文。

• 选择明文攻击

  如果可以对任意密文解密，但不能对 C 解密，可以求出 C 的 N 上 d 的逆元 C^{-1，然后求 C}-1 的明文 M'。M' 即为明文的逆元，再次求逆即可。

• LLL-attack

  在已知 e 且 e 较小的情况下，如果已经泄露了一部分密文（例如在信息开头打招呼），或者泄露了 p 或 q 的一部分，又或者是直接泄露了一部分明文的 bit，当泄露的信息长度足够时，可以通过 Coppersmith method 的方法求得明文。

• Wiener Attack & Boneh Durfee Attack

  如果 e 很大但生成的 d 过下，也会被成功攻击，即 RSA Wiener Attack。

• 共模攻击

  如果在两次通讯中使用了相同的 n，并且是对相同的 m 加密，那么可以不计算 d 直接计算出 m 的值。

  即当又两组及以上的 RSA 加密过程，其中两次的 m 和 n 都是相同的，就可以通过计算直接计算出 m。

• 广播攻击

  在连续进行 RSA 加密时，如果选择的加密指数 e 较小，并且每次加密的信息都是相同的，可以通过中国剩余定理计算出一个数 c^{e，这时对 c}e 开 e 次根号就可以得到 m。

• 相关消息攻击

  如果用同一公钥对两个具有某种线性关系的消息 m1 和 m2 进行加密。当 e 比较小时，就可以根据加密后的 c1 和 c2 九三出相应的 m1 和 m2.

# 哈希

哈希，也叫散列，可以把任意长度的输入，变换成固定长度的输出，输出结果即为哈希值。这种转换是一种压缩映射，即哈希值的空间通常远小于输入的空间，导致不同的输入可能会拥有相同的哈希值，所以不能通过哈希值来唯一确定输入值。。

哈希函数有很多，常见的有 MD5、sha1、sha256 等。

# 哈希函数的攻击

• 哈希碰撞（暴力攻击）

  不依赖于任何算法细节，暴力破解明文，仅与 Hash 值长度有关。

• 哈希长度扩展攻击

  在计算 hash 的方式 secret+message 为明文的情况下，可以进行哈希长度扩展攻击，使攻击者可以在不知道 secret 的情况下修改 message 并得到另外一个 hash 值。